Table of Contents
Understanding Low-Rank Adaptation (LoRA)
Before we delve into Low-Rank Adaptation (LoRA), let’s briefly revisit the basics. In the transformer architecture, input prompts are tokenized, converted to embedding vectors, and then passed into the encoder and/or decoder parts. Two types of neural networks are utilized in these components: self-attention and feedforward networks. These networks’ weights are learned during pre-training.
LoRA is a technique of PEFT to learn about PEFT with coding example visit the link: click here
The Concept of LoRA
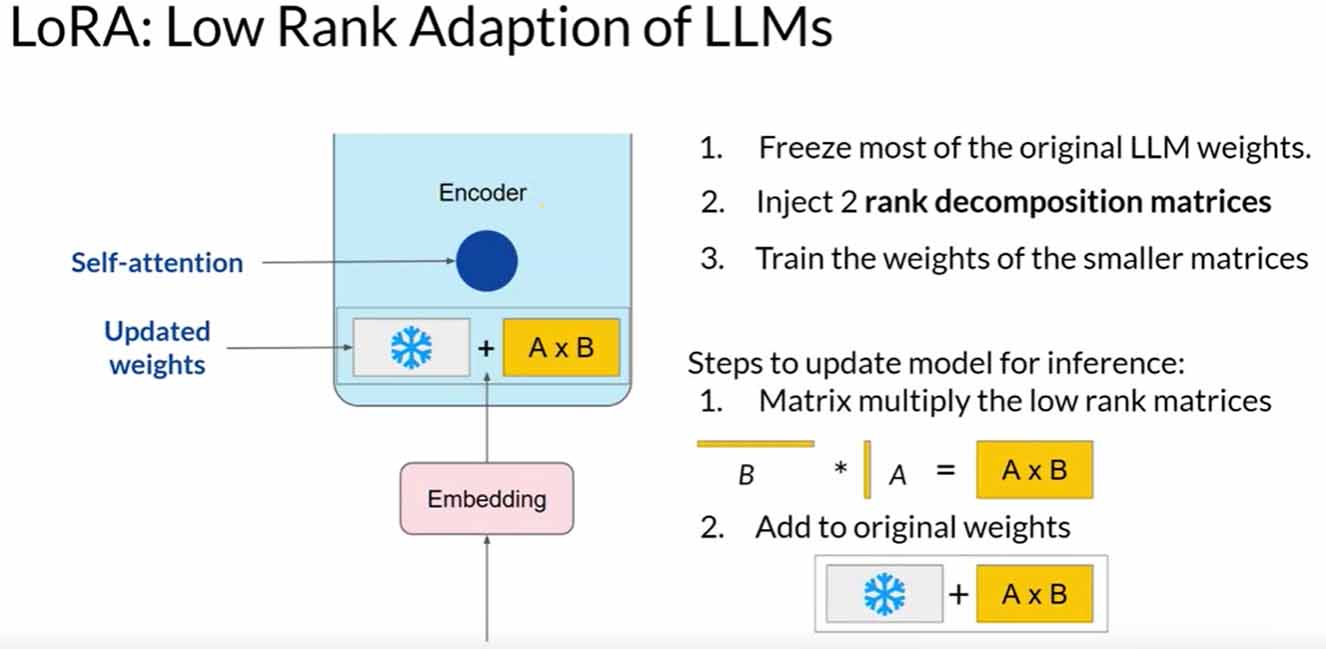
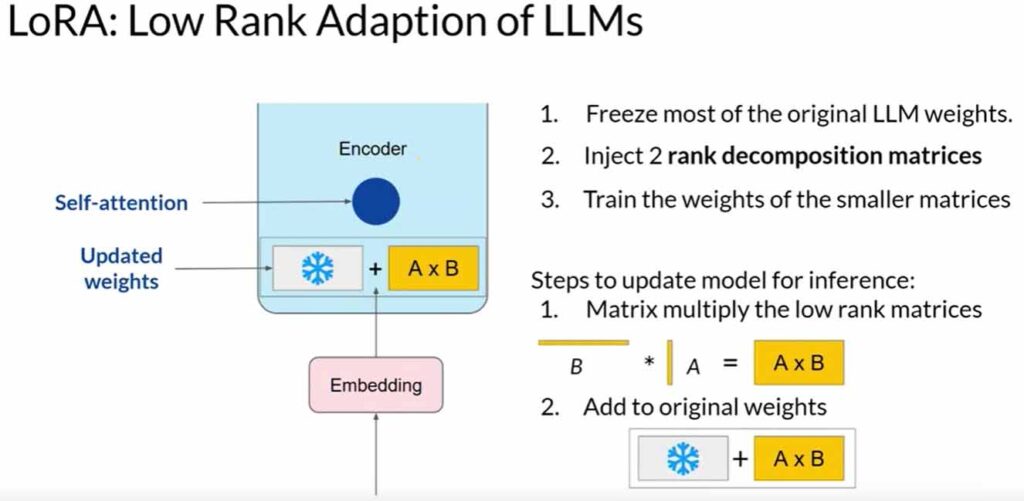
LoRA aims to reduce the number of trainable parameters during fine-tuning. It involves freezing all original model parameters and introducing a pair of rank decomposition matrices alongside the weights. These smaller matrices are designed to have dimensions that match the weights they modify.
Applying LoRA to Fine-Tuning
During full fine-tuning, every parameter in the self-attention and feedforward layers is updated. LoRA, on the other hand, selectively updates only the smaller matrices while keeping the original weights frozen. Research has shown that applying LoRA to just the self-attention layers can achieve significant performance gains.
A Practical Example with Transformer Architecture
Let’s explore a practical example using the transformer architecture from the “Attention is All You Need” paper. Suppose the transformer weights have dimensions of 512 by 64, resulting in 32,768 trainable parameters. By employing LoRA with a rank equal to eight, we train two small rank decomposition matrices. Matrix A (8×64) will have 512 parameters, and Matrix B (512×8) will have 4,096 parameters. This leads to training only 4,608 parameters, an 86% reduction compared to full fine-tuning.
Coding Example for Low-rank adaptation (LoRA)
Low-rank adaptation is a technique used in machine learning to adapt a pre-trained model to a specific task or domain while reducing the model’s dimensionality, typically through matrix factorization or other low-rank approximations. This can help make models more efficient and reduce the risk of overfitting. Here’s a high-level code example demonstrating low-rank adaptation using Python and NumPy:
import numpy as np
// Suppose you have a pre-trained model represented as a weight matrix W
pretrained_model = np.random.randn(100, 100) // Example: 100x100 weight matrix
// Define your task-specific data and labels
X = np.random.randn(100, 10) // Example: 100 samples, 10 features
y = np.random.randint(0, 2, size=(100,)) // Example: Binary classification labels
// Perform low-rank adaptation using Singular Value Decomposition (SVD)
U, S, Vt = np.linalg.svd(X, full_matrices=False) // Perform SVD on the data matrix X
// Define a low-rank approximation rank
rank = 20 // You can choose an appropriate rank based on your needs
// Create a low-rank approximation of the weight matrix W
low_rank_W = np.dot(U[:, :rank], np.dot(np.diag(S[:rank]), Vt[:rank, :]))
// Now you can use low_rank_W for your task-specific model
// Example: You might use logistic regression with low_rank_W as weights
from sklearn.linear_model import LogisticRegression
lr_model = LogisticRegression()
lr_model.fit(low_rank_W.dot(X.T).T, y) // Training using the low-rank adapted weights
// Make predictions using the adapted model
y_pred = lr_model.predict(low_rank_W.dot(X.T).T)
In this code example:
- We start by assuming you have a pre-trained model represented as a weight matrix
pretrained_model. - You have task-specific data
Xand labelsy. - We perform low-rank adaptation using Singular Value Decomposition (SVD) on the data matrix
X. The SVD decomposition provides the matricesU,S, andVt. - You can choose a low-rank approximation by selecting the top
ranksingular values and vectors fromU,S, andVt. - We create a low-rank approximation of the weight matrix
low_rank_Wby multiplying these selected matrices. - Finally, you can use
low_rank_Was weights for a task-specific model, such as logistic regression in this example, and make predictions.
Please note that this is a simplified example, and in practice, you might want to fine-tune the low-rank approximation for your specific task and experiment with different values of the rank. The actual implementation may vary depending on the libraries and tools you are using for your machine learning tasks.
Performance Comparison of Low-Rank Adaptation (LoRA)
LoRA achieves a substantial boost in performance without significantly increasing the number of trainable parameters. Comparing LoRA fine-tuned models to both the original base model and full fine-tuned versions using the ROUGE metric shows impressive results. While full fine-tuning provides a slightly higher ROUGE 1 score, LoRA’s benefits in parameter efficiency and compute make it an appealing alternative.
Choosing the Rank for LoRA
Selecting the rank for LoRA matrices is crucial, as it affects the trade-off between reducing trainable parameters and preserving performance. Studies indicate that ranks in the range of 4-32 strike a good balance, providing substantial parameter reduction without sacrificing performance.
LoRA Beyond Language Models
LoRA’s principles extend beyond just training Language Models (LLMs). Its application can be adapted to various models and domains, making it a versatile technique with promising potential.
Conclusion
Low-Rank Adaptation (LoRA) proves to be a powerful parameter-efficient fine-tuning method, significantly reducing the number of trainable parameters while maintaining performance. Its adaptability and benefits extend beyond language models, making it an essential tool for researchers and practitioners alike.
FAQs:
Q1: Can LoRA be applied to other components in addition to self-attention layers?
Yes, in theory, LoRA can be applied to other components like feedforward layers. However, since most parameters in Language Models are in the attention layers, applying LoRA to these weights matrices yields the most significant savings in trainable parameters.
Q2: How do I choose the rank for LoRA matrices?
Choosing the rank for LoRA is an ongoing area of research. Studies suggest that ranks in the range of 4-32 can provide a good trade-off between reducing trainable parameters and preserving performance.
Q3: Can I use LoRA for multiple tasks?
Yes, you can fine-tune a different set of LoRA matrices for each specific task and switch them out during inference, avoiding the need to store multiple full-size versions of the Language Model.
Q4: Is LoRA limited to Language Models only?
No, LoRA’s principles are applicable to various models and domains, making it a valuable technique beyond language models.
Q5: How does LoRA compare to full fine-tuning in terms of performance?
LoRA achieves slightly lower ROUGE scores compared to full fine-tuning. However, the significant reduction in trainable parameters and compute requirements makes LoRA an attractive option for many applications.